Number Theory Generator

Instructions below example images:

PolicyID: f683c3bda525744e5848789c615fe3fa4cc5e38e96f8c71c18d4e5db

Secondary JPG.Store: NumberTheoryGenerator NFTs | JPG Store

Secondary Plutus.art Plutus | Art

Small selection of outputs from the Number Theory Generator

Why? I really like generative art, and i really like the challenge of OnChain art on Cardano – This limits your code to <14Kb in size. And also means not referencing any external library/code. Ive also always enjoyed visualisation of number patterns, so i put the two things together. I want to give myself and others the opportunity to explore number theory, and at the same time explore its impact on art.

There are three modes of NFT in the collection, Generator, Fixed and Random:

Generator

The instructions below are for Generator mode – this mode allows you to create any output in the collection, but you need to set the parameters as per the instructions below. This mode does not auto generate an image for you, but gives you full creative control. You can copy the metadata of any other image in the collection to recreate it.

Fixed

Fixed mode has parameters ‘fixed’ which will mean the output will be the same each time the on chain code is refreshed, except for colours and backgrounds.

Example: NumberTheoryGenerator0234 (pool.pm)

Random

Random mode has some parameters fixed, but some randomly set each refresh. So every time you reload the code, it will generate a new output with new parameters.

Generator Instructions

You can test the instructions out below on chain, here: NumberTheoryGenerator0001 (pool.pm)

OK, so the Number Theory Generator is confusing at first glance. It wont do much on first loading the page until you select some options and functions. It will only draw a background to start.

So the first thing to do it select the Base. The default Base is 10. This means two things for our image, the number of columns or blocks across, and in rotation mode the number of points on the rotation. Think the number of points on a clock.

The image width will determine the number or rows as well as the number of pixels in the image.

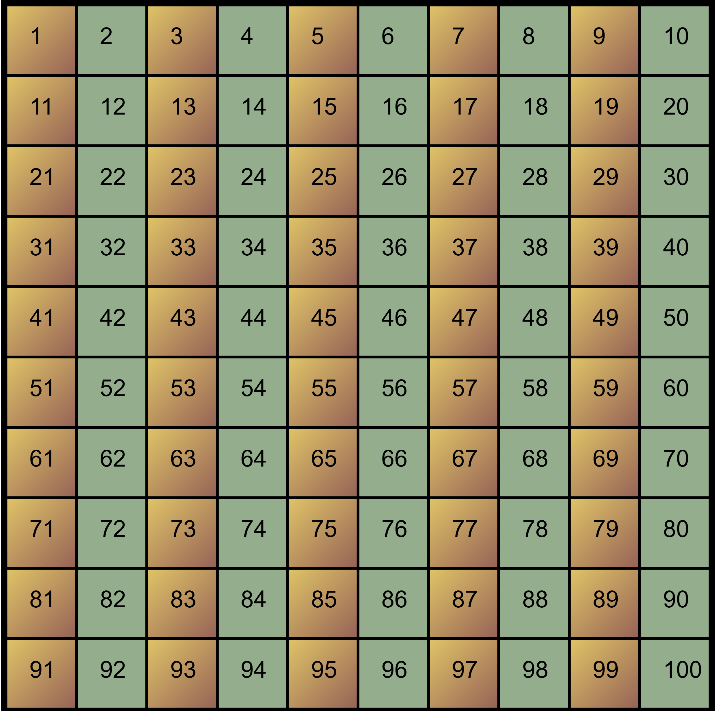
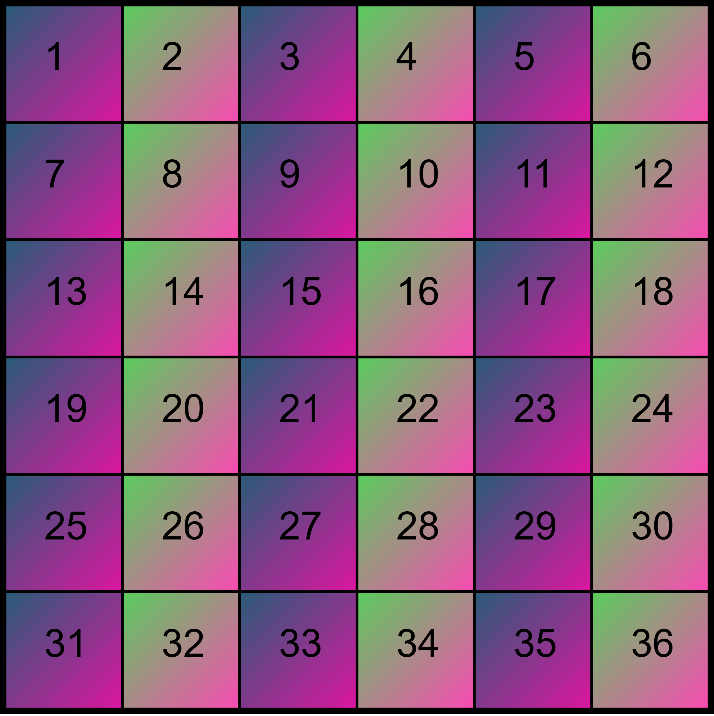
One you have a Base, height and width set you need to reset the image for the change to take effect.

You can then set the visual controls on the first line of UI such as Overlay and Shape.

Circle and Diamond shapes, with Text set to on

Change will change the colour used to draw a shape. If unset, the same colour is continued to be used for all function calls.

Border will draw a border square around the matching numbers.

Text will set the number will be draw at the centre of the shape.

Overlay, if this is set the drawing will have alpha set so it is transparent.

Connect draws a line connecting the path of shapes.

Arrow draws a vertical or horisonal line to identify the matching numbers.

Enlarge will increase the size of the line or shape drawn for larder bases.

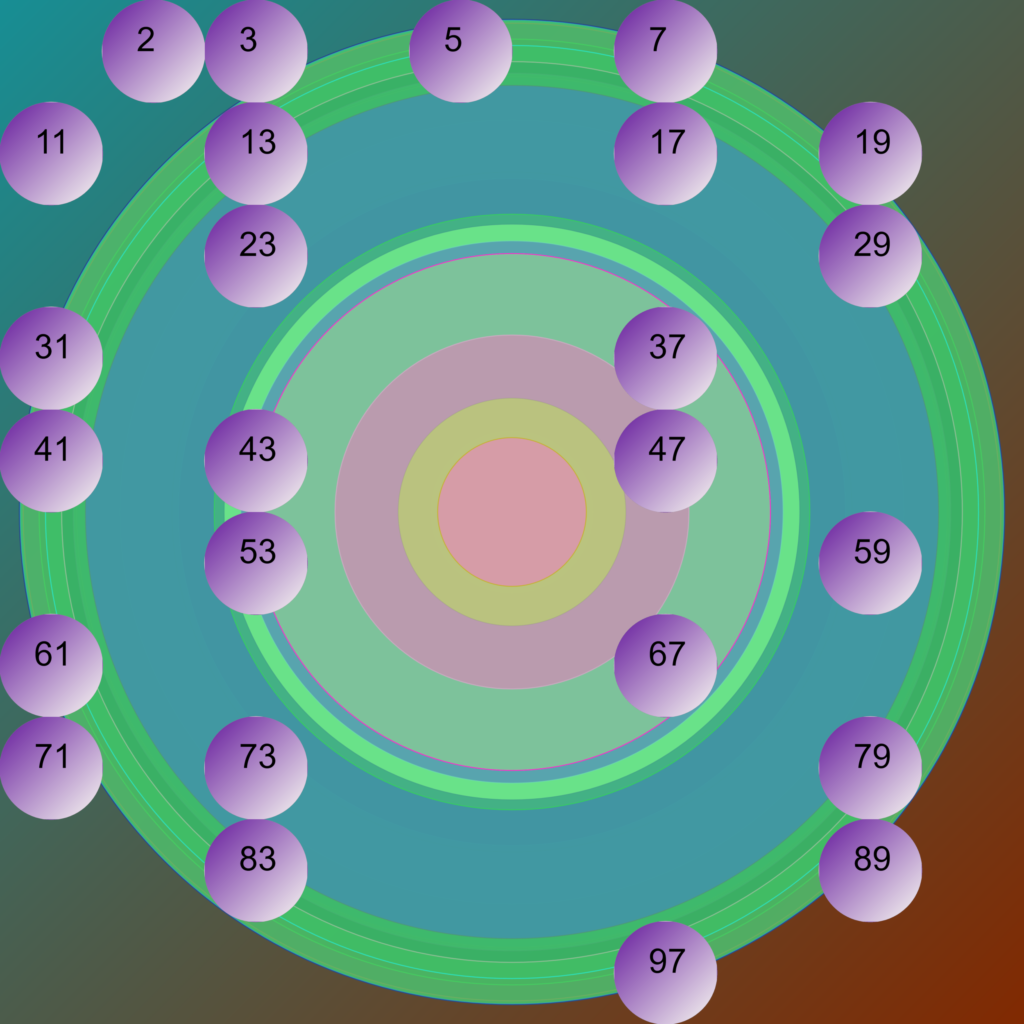
Shapes can be seen on the images on this page, include Rectangle, Circle, Diamond and Rotation.

Metadata:{“grid”:”123×123″,”background”:”SolidColour”,”functions”:”Modulus(3)”,”style”:”Rotation, Enlarged Rotation”}

Metadata:{“grid”:”10×4″,”background”:”SolidColour”,”functions”:”Odds, Evens”,”style”:”Rectangle on grid with text”}

The metadata is designed to provide instruction to repeat an output, and will allow users to mint outputs into the collection.

Functions

The Arithmetic button will show the arithmetic progression of f(x). So you can set the f(x) value and then see it repeat. You can then overlay multiple arithmetic progressions. For example here is base 20 with arithmetic 7

Geometric Sequence will set the geometric sequence of f(x). A Geometric Sequence is made by multiplying by the same value each time.

Metadata:{“grid”:”100×100″,”background”:”Gradient”,”functions”:”Geometric(3)”,”style”:”Circle connected”}

Modulus is only really useful when Shape is set to rotation, as its a sequence. Below shows modulus 2 with a base 200.

Metadata:{“grid”:”200×200″,”background”:”Concentric Prime”,”functions”:”Modulus(2)”,”style”:”Rotation, Enlarged Rotation”}

This Triangular Number Sequence is generated from a pattern of dots that form a triangle.

Metadata:{“grid”:”1000×1000″,”background”:”Gradient”,”functions”:”Square”,”style”:”Circle connected with arrows”}

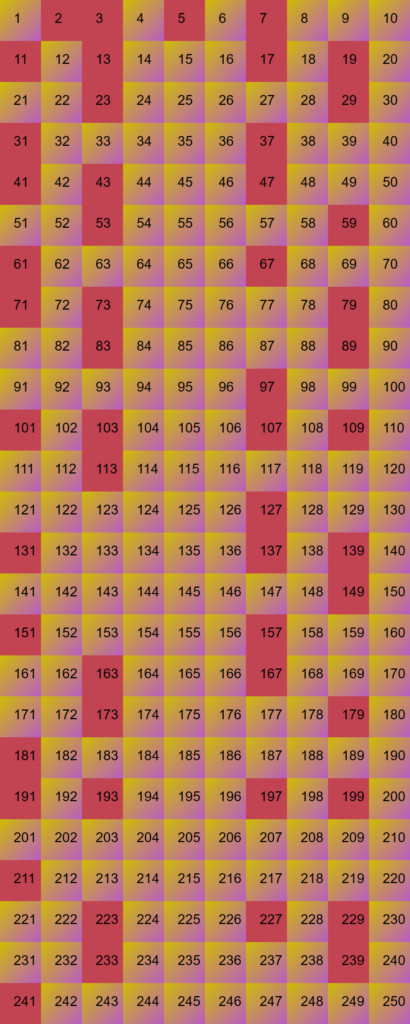
Prime numbers need no introduction, but the Composite may. Composite numbers are simply non-prime numbers.

Metadata:{“grid”:”1000×1000″,”background”:”Gradient”,”functions”:”Prime”,”style”:”Circle”}

Metadata:{“grid”:”10×25″,”background”:”SolidColour”,”functions”:”Prime, Composite, Prime”,”style”:”Rectangle with text”}

The Fibonacci Sequence is found by adding the two numbers before it together.

Metadata:{“grid”:”10×100″,”background”:”SolidColour”,”functions”:”Fibonacci”,”style”:”Rectangle with text”}

Palindromes are numbers which when written read the same in both directions.

Metadata:{“grid”:”500×500″,”background”:”SolidColour”,”functions”:”Palindromes”,”style”:”Circle”}

There are also some special backgrounds: